최단 경로 문제는 시간 또는 비용의 합이 최소가 되는 경로를 찾는 문제다.

회사에서 편의점을 거쳐서 오면 1시간이 걸리고,
회사에서 헬스장을 가쳐서 오면 1시간 30분이 걸린다면,
편의점을 거쳐 집으로 오는 길, 즉 제일 빠른 길 탐색하는 문제다.
코딩 테스트에서 최단 경로 문제는 주로 다익스트라 알고리즘으로 구현한다.
다익스트라 알고리즘은 정점(vertex) 주변의 최단 경로만 택하는 알고리즘이다.
단순할 뿐만 아니라 실행 속도도 빠른 장점이 있다.
'회사'를 정점으로 하면 주변은 헬스장과 편의점이 있고 최단 경로는 편의점으로 가는 길인 셈이다.
다익스트라 알고리즘은 너비우선탐색(BFS)를 이용하는 대표적 알고리즘이다.
허접하게 비유하자면,
회사에서 편의점을 거쳐 집까지 쭉 판 다음, 헬스장에 간다면 깊이 우선 탐색(DFS)이고,
편의점과 헬스장을 차례로 거친 다음, 집을 탐색한다면 너비 우선 탐색(BFS)이다.
다익스트라 알고리즘의 기본 메커니즘은 동영상으로 설명하는 게 가장 이해가 잘 되었다.
추천 영상을 링크를 아래에 붙인다.
https://www.youtube.com/watch?v=qaiuC3Q73-M
그러면 본격적으로 리트코드 743번 '네트워크 딜레이 타임' 문제를 다익스트라 알고리즘으로 풀어보자
참고로 문제 자체가 좀 어려워서 이해하는 데 한참 걸렸다.
아래 그림을 통해 보면,
2번 노드(변수 K)에서 출발하여 화살표 방향으로 신호를 보내는 데,
화살표 위에 숫자만큼 시간이 걸린다.
모든 노드가 신호를 받을 때 걸리는 최소 시간을 구하는 문제다
(계산이 불가능할 경우 -1을 리턴한다)
결론부터 말하면 정답은 '2'다
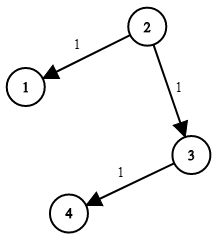
입력값과 출력값은 아래와 같다.
Input: times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
Output: 2
times 변수에 할당된 2차원 리스트의 요소들( [ u, v, w ] )에서,
u는 출발 노드
v는 도착 노드
w는 걸리는 시간이다.
예를 들어, [ 2, 1, 1 ]은 2번 노드에서 1번 노드까지 '1'이라는 시간이 걸린다는 말이다.
또 다른 입력값 n은 노드의 개수(위 예제에서는 4개)를 뜻하고,
k는 출발 노드(위에서 2번)이다.
문제 풀이는 우선순위 큐를 사용한다. 구체적으로 한번 살펴보자
1. 우선 함수를 정의하고 그래프의 인접 리스트를 구성한다

변수 'items'의 자료형을 리스트에서 딕셔너리로 바꿔주기 위해서,
defualtdict 객체를 생성한다.
출발 노드(u)를 키(key)로,
도착 노드 및 소요 시간(v, w)을 값(value)으로 하는 딕셔너리 형태로 변환한다.
참고로 times 리스트를
딕셔너리 형태로 변환하면 출력 값은 아래와 같이 변한다.

2. 힙큐 리스트를 정의한다.
참고로 Q = [ ( 소요 시간, 정점) ] 구조이다.

앞으로 최단 경로를 채워나갈 리스트라고 보면 된다.
3. 변수 'dist'에 딕셔너리를 새로 정의한다.

'dist'는 추후 모든 경로에 대해서 최단 경로가 존재하는지 유무를 판단하고,
존재할 때 걸리는 시간을 도출하는 데 사용된다
4. 각 정점까지 최단경로를 구해서 dist에 삽입한다. min heap을 기준으로 적용한다.

우선 Q(min heap)가 빌 때까지 반복 연산을 하기 위하 while문을 이용한다.
heappop 메서드를 이용하여 최소 시간이 걸리는 노드를 우선적으로 추출한다.
추출된 노드가 dist에 없다면,
그런 다음 이동할 노드(node)와 소요시간(time)의 위치를 서로 바꾸어 'dist'에 저장한다.
그런 다음 'for 문'을 이용하여,
추출된 노드와 연결되는 다른 노드들을 heapq에 올려준다.
다시 heapq에서 최소 시간이 걸리는 노드를 추출하는 방식으로 노드가 반복된다.
위 과정을 그림으로 나타내면 다음과 같다.
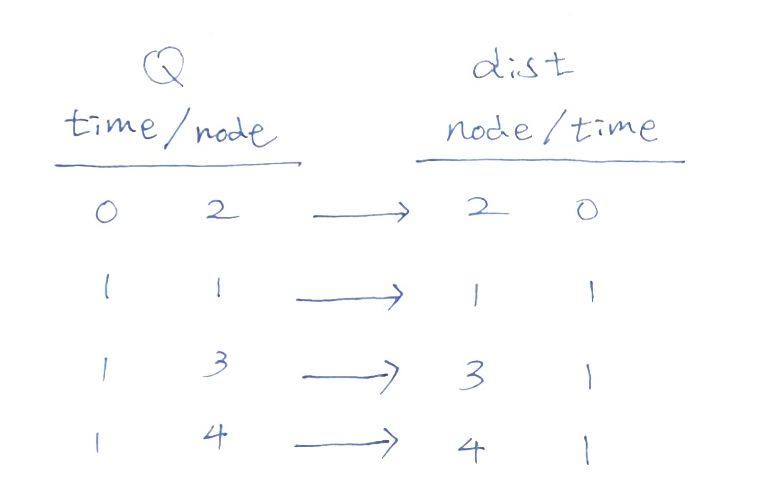
모든 노드의 시간이 1이기 때문에,
heap에서 추출된 값이 heap에서 추가됐던 순서대로
dist에 옮겨진다.
만약 노드마다 시간이 다르다면,
시간이 제일 짧은 노드 먼저 추출되어 dist로 옮겨질 것이다.
5. 모든 경로가 최단 경로에 포함되는지 여부를 판단하고 최대 시간을 출력한다.

앞서 말했듯이 N은 전체 노드의 개수다.
dist의 길이가 N과 같다는 말은 모든 노드가 디스트로 다 옮겨졌다(최단 경로에 포함되었다)는 말이다.
조건이 성립할 경우, dist의 값(value) 중 최대 값을 리턴한다.
이 값이 곧 모든 노드에 신호를 보내는 데 소요되는 시간이다.
위 조건을 충족하지 못한다면 -1을 리턴한다.
* 위 내용은 '파이썬 알고리즘 인터뷰(박상길 / 책만)의 해설을 토대로 작성했습니다.
'자료구조 & 알고리즘' 카테고리의 다른 글
| 비트 조작 - 부울 연산자, 비트 연산자, 2의 보수 개념 (0) | 2022.06.18 |
|---|---|
| [파이썬] 초기화 함수 / __init__() 메서드는 왜 쓰는 걸까? (0) | 2022.05.16 |
| 트리 순회 - 전위(Pre-Order), 중위(In-order), 후위(post-Order) 순회 (0) | 2022.04.28 |
| 비전공자 코딩 테스트 공부법 - 파이썬 알고리즘 인터뷰 (0) | 2022.04.14 |
| [자료구조 ] 이진 트리 - 그래프와 차이점, 명칭, 종류 (0) | 2022.04.07 |