다이나믹 프로그래밍(Dynamic Programming) 알고리즘을 피보나치수열을 예로 들어 설명해보려 한다.
해당 문제는 리트코드(LeetCode) 85번 문제를 참조하면 된다.
< 목차 >
1. 다이나믹 프로그래밍의 의미
2. 다이나믹프로그래밍의 특성
3. 다이나믹프로그래밍 방법론
4. 다이나믹프로그래밍 의의
1. 다이나믹 프로그래밍 의미
다이나믹 프로그래밍(Dynamic Programming)이란 하나의 문제를 여러 개의 하부 문제로 분할하고,
하부 문제를 해결하고 그 결과를 저장하여,
전체 문제 풀이에 더해가며 문제를 해결하는 알고리즘이다.
2. 다이나믹 프로그래밍의 특성
다이나믹 프로그래밍으로 해결할 수 있는 문제는 두 가지 특성을 충족해야 한다.
1. 부분 최적 구조(Optimal Substructure)
전체 문제의 최적 해결 방법이 부분 문제의 최적 해결 방안으로 구성됨을 의미한다.
2. 중복된 하위 문제(Overlapping Sub-problem)
전체 문제를 풀이하는 과정이 여러 번 나타나는 하부 문제 해답으로 구성되는 구조를 말한다.

피보나치수열 예시를 통해 앞서 말한 두 가지 특성을 알아보자.
피보나치수열은 이전 두 개의 값을 더하여 새로운 값을 구하는 방식이며,
수식으로 표현하면 다음과 같다.
F(n) = F(n-1) + F(n-2)
F(0) = 0이고, F(1) =1일 때, F(2)는 F(1)과 F(2)를 더한 값, 즉 2가 된다.
피보나치수열은 하부 문제를 해결함으로써 전체 문제에 대한 답을 구할 수 있다.(최적 부분 구조)
위에서 말한 수식으로 F(0)부터 계산을 해나가면 그림 상 맨 꼭대기에 있는 F(4)를 구할 수 있다.
위 그림에서 F(2)의 경우 꼭대기 F(4)를 기준으로 왼쪽에도 존재하고 오른쪽에도 존재한다.
즉 F(4)를 구하기 위해 F(2)가 중복해서 계산이 되는 구조다.(중복된 하위 문제)
3. 다이나믹 프로그래밍 방법론
동적 프로그래밍 알고리즘을 이용하여 문제를 해결하는 방법에는 크게 두 가지가 있다.
1. 상향식(Bottom-Up)
타뷸레이션(tabulation) 이라고도 한다.
하위 문제를 먼저 계산한 후, 그 값을 메모리에 저장해둔다.
저장된 하위 문제 값을 토대로 전체 문제 값을 계산해나간다.
일반적으로 반복적(Iterative) 방법을 이용해서 구현한다.
2. 하향식(Top-Down)
메모이제이션(Memoization)이라고도 부른다.
일반적으로 재귀적(Recursive) 방법으로 계산하며,
이전에 계산된 하부 문제 값이 존재하는지 참조하며 재귀 호출을 진행하는 방식이다.
아래는 두 가지 방법으로 피보나치수열을 구현한 코드다.
(손으로 지저분하게 작성한 점 양해 바란다)

4. 다이나믹 프로그래밍 의의
타뷸레이션과 메모이제이션을 활용하면 미리 저장된 하부 문제의 답을 참조할 수 있기 때문에 연산 과정이 빨라진다.

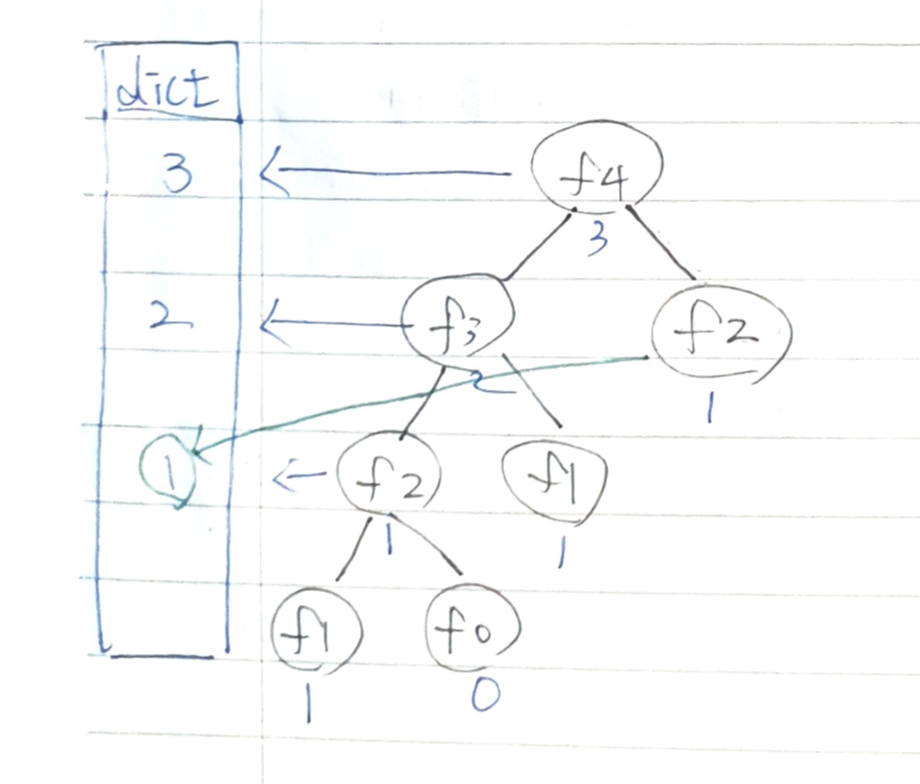
왼쪽은 브루트 포스 방식으로 구현한 피보나치수열이고, 오른쪽은 다이나믹 프로그래밍(타뷸레이션, 메모이제이션)으로 구현한 그래프다.
왼쪽 그림에서는 모든 경우의 수를 다 적용하여 해답(f(4))을 구한 방식을 그래프로 나타냈다.
반면 오른쪽 그래프에서 꼭대기를 기준으로 오른쪽 부분을 보면 일부가 잘려 있음을 알 수 있다.
f(2)의 경우 꼭대기 기준 왼쪽 부분에서 하부 문제로 해답을 이미 구했기 때문에,
오른쪽에서는 f(2)를 다시 쪼개어 정답을 구하지 않고 왼쪽 f(2) 값을 참조한 것이다.
이처럼 다이나믹 프로그래밍 알고리즘으로 '최적 부분 구조' 및 '중복 하부 문제'의 특성을 지닌 문제를 효율적으로 풀 수 있다.
* 본 포스팅은 도서 '파이썬 알고리즘 인터뷰(책만 / 박상길)'을 참조하여 작성했습니다.
'자료구조 & 알고리즘' 카테고리의 다른 글
| [파이썬] 스택 - 일일 온도(리트코드 739) (0) | 2022.07.07 |
|---|---|
| 분할 정복 예제 - 과반수 엘리먼트(리트코드 169) (0) | 2022.07.03 |
| 비트 조작 - 부울 연산자, 비트 연산자, 2의 보수 개념 (0) | 2022.06.18 |
| [파이썬] 초기화 함수 / __init__() 메서드는 왜 쓰는 걸까? (0) | 2022.05.16 |
| 트리 순회 - 전위(Pre-Order), 중위(In-order), 후위(post-Order) 순회 (0) | 2022.04.28 |